 Uncategorized
Uncategorized AT ProtocolのRepositoryに関して調査・考察
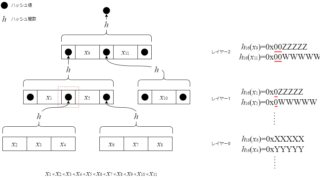
前回AT Protocolでよく出てくるCBOR・CID・DAG-CBORについて調査・まとめました。これらがAT Protocol中で主に出てくるのはRepositoryに関する仕様の部分です。今回はRepositoryとは何か、Rep...
 Uncategorized
Uncategorized  Uncategorized
Uncategorized  Uncategorized
Uncategorized  Uncategorized
Uncategorized  コンピュータアーキテクチャ
コンピュータアーキテクチャ  Uncategorized
Uncategorized  Uncategorized
Uncategorized  Uncategorized
Uncategorized  Uncategorized
Uncategorized  コンピュータアーキテクチャ
コンピュータアーキテクチャ